O cortador de grama motorizado possui uma massa de , com centro de massa em . O operador possui uma massa de , com centro de massa em . Calcule o coeficiente de atrito efeivo mínimo que permitirá as rodas dianteiras do cortados se levantarem do solo quando o cortador começar a se deslocar para a frente.
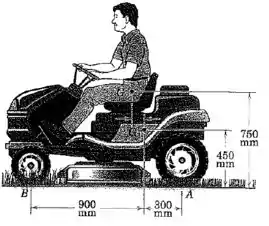
Passo 1
Quando o cortador está prestes a erguer suas rodas dianteiras, a força normal no ponto se aproxima de zero, e as forças estão em equilíbrio na vertical (já que o sistema não acelera nesse direção):
Passo 2
Agora vamos supôr que, quando o operador começa a se deslocar para frente, o sistema inteiro adquire uma aceleração para frente.
Nesse caso, existem forças resultantes agindo sobre os centros de massa do operador e do cortador:
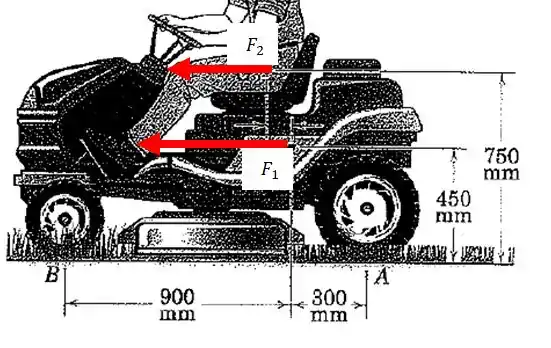
Então o momento resultante que age sobre o corpo será:
Onde e são as distâncias perpendiculares entre os pontos de aplicação das forças e o ponto de referência que escolhermos.
Nesse caso, seria conveniente escolher o ponto como referência, para eliminar a força que é desconhecidam, então:
E quando escolhemos o ponto , os únicos momentos serão os dos pesos e , que agem nos centros de massa e :
E então:
Passo 3
Agora vamos analisar a força resultante na direção horizontal:
E a força agindo nessa direção, quando as rodas dianteiras estão prestes a perder contato com o chão, é a força de atrito na roda :
Como nesse momento o único apoio do sistema no chão é pela roda , essa força deve suportar todo o peso:
Então:
Resposta
O coeficiente de atrito mínimo deve ser .